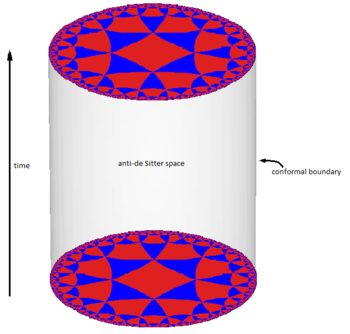
My research interests are very broad and I hope to be able to work on many different things during my PhD. So far, I have mostly worked on conformal field theories, in particular on various ways of constraining their spectrum. I have done work in 2d and in higher dimensions and I am particularly interested in the bootstrap ideas (conformal and modular). I like to think about holography, either from the CFT point of view or from the information theory version of the statement. I have worked on topological defects during my undergraduate studies and I am still interested in that. This page contains information about the research that I did since I came to McGill.
Details about research that I did during my undergrad can be found here.
A list of my publications is available on inspire.
Quantum Regge Trajectories and the Virasoro Analytic Bootstrap
Every conformal field theory (CFT) above two dimensions contains an infinite set of Regge trajectories of local operators which, at large spin, asymptote to "double-twist" composites with vanishing anomalous dimension. In two dimensions, due to the existence of local conformal symmetry, this and other central results of the conformal bootstrap do not apply. We incorporate exact stress tensor dynamics into the CFT2 analytic bootstrap, and extract several implications for AdS3 quantum gravity. Our main tool is the Virasoro fusion kernel, which we newly analyze and interpret in the bootstrap context. The contribution to double-twist data from the Virasoro vacuum module defines a "Virasoro Mean Field Theory" (VMFT); its spectrum includes a finite number of discrete Regge trajectories, whose dimensions obey a simple formula exact in the central charge c and external operator dimensions. We then show that VMFT provides a baseline for large spin universality in two dimensions: in every unitary compact CFT2 with c greater than 1 and a twist gap above the vacuum, the double-twist data approaches that of VMFT at large spin J. Corrections to the large spin spectrum from individual non-vacuum primaries are exponentially small in sqrt(J) for fixed c. We analyze our results in various large c limits. Further applications include a derivation of the late-time behavior of Virasoro blocks at generic c ; a refined understanding and new derivation of heavy-light blocks; and the determination of the cross-channel limit of generic Virasoro blocks. We translate our results into statements about quantum gravity in AdS3.
Reference: arXiv: 1811.05710 [hep-th]
I gave a journal club at McGill about the paper and the slides are here
Thermal conformal blocks
We study conformal blocks for thermal one-point-functions on the sphere in conformal field theories of general dimension. These thermal conformal blocks satisfy second order Casimir differential equations and have integral representations related to AdS Witten diagrams. We give an analytic formula for the scalar conformal block in terms of generalized hypergeometric functions. As an application, we deduce an asymptotic formula for the three-point coeffcients of primary operators in the limit where two of the operators are heavy.
Reference: arXiv: 1802.10537 [hep-th]
You can find here the slides of a short talk that I gave on this paper at ICMP 2018.
Constraints on the spectrum of operators in two-dimensional Conformal Field Theories (Master's thesis)
During my Master's I worked on two different things, both in the context of 2d CFT. First of all I studied consequences of modular invariance of the torus partition function on the spectrum of CFTs. Constraints from the S and the ST transformations have already been found and they lead to upper bounds on the dimension of primary operators. The work that I did is find the constraint coming from a general modular transformation. The hope is that combining this infinite number of constraints into a new one would allow us to improve the known bound. The second thing that I studied in the past year is W-algebras, which are extensions of the Virasoro algebra with higher spin generators. I worked specifically with W(2,4) and found constraints on the dimension and the charge of primary states that are allowed in a unitary theory. These constraints are found by studying the Gram matrix of the first few levels of a highest weight representation of the algebra.
Here is a talk that I gave at the CAP congress in June 2016 about W-algebra bounds.